Die Lag-Länge in VAR-Modellen (Vektorautoregression) ist ein wichtiger Faktor, der die Genauigkeit des Modells beeinflusst. Das Verständnis der Ergebnisse von Lag-Längen-Auswahltests in VAR hilft uns, die optimale Anzahl an Lags zu bestimmen und sicherzustellen, dass das VAR-Modell effektiv arbeitet. Dieser Artikel führt Sie durch die Interpretation der Ergebnisse von Lag-Längen-Auswahltests in VAR und deren praktische Anwendung.
Bedeutung der Wahl der VAR-Lag-Länge
Die richtige Wahl der Lag-Länge in einem VAR-Modell ist äusserst wichtig. Wenn zu wenige Lags gewählt werden, erfasst das Modell nicht alle dynamischen Beziehungen zwischen den Variablen, was zu fehlerhaften Ergebnissen führt. Umgekehrt kann die Wahl von zu vielen Lags das Modell unnötig komplex und schwer interpretierbar machen und zu Overfitting führen. Die Lag-Längen-Auswahltests helfen uns, ein Gleichgewicht zwischen der Genauigkeit und der Komplexität des Modells zu finden.
Methoden zur Bestimmung der optimalen VAR-Lag-Länge
Es gibt verschiedene Testmethoden, um die optimale Lag-Länge für ein VAR-Modell zu bestimmen. Einige gängige Methoden sind:
- Akaike-Informationskriterium (AIC): Diese Methode sucht nach der Lag-Länge, die den AIC-Wert minimiert.
- Bayesianisches Informationskriterium (BIC) oder Schwarz-Kriterium (SC): Ähnlich wie das AIC sucht das BIC/SC nach der Lag-Länge, die den BIC/SC-Wert minimiert. BIC/SC bevorzugt in der Regel einfachere Modelle als AIC.
- Likelihood-Ratio-Test (LR-Test): Dieser Test vergleicht Modelle mit unterschiedlichen Lag-Längen, um festzustellen, ob eine Reduzierung der Lag-Länge die Erklärungskraft des Modells signifikant verringert.
Interpretation der Testergebnisse
Die Testergebnisse werden üblicherweise in Tabellenform dargestellt, wobei jede Zeile eine Lag-Länge und jede Spalte ein Informationskriterium (AIC, BIC/SC, HQIC usw.) repräsentiert. Die Lag-Länge, die dem kleinsten Wert des Informationskriteriums entspricht, wird als optimale Lag-Länge betrachtet. Wenn beispielsweise der kleinste AIC-Wert bei Lag-Länge 2 liegt, sollten wir Lag-Länge 2 für das VAR-Modell wählen.
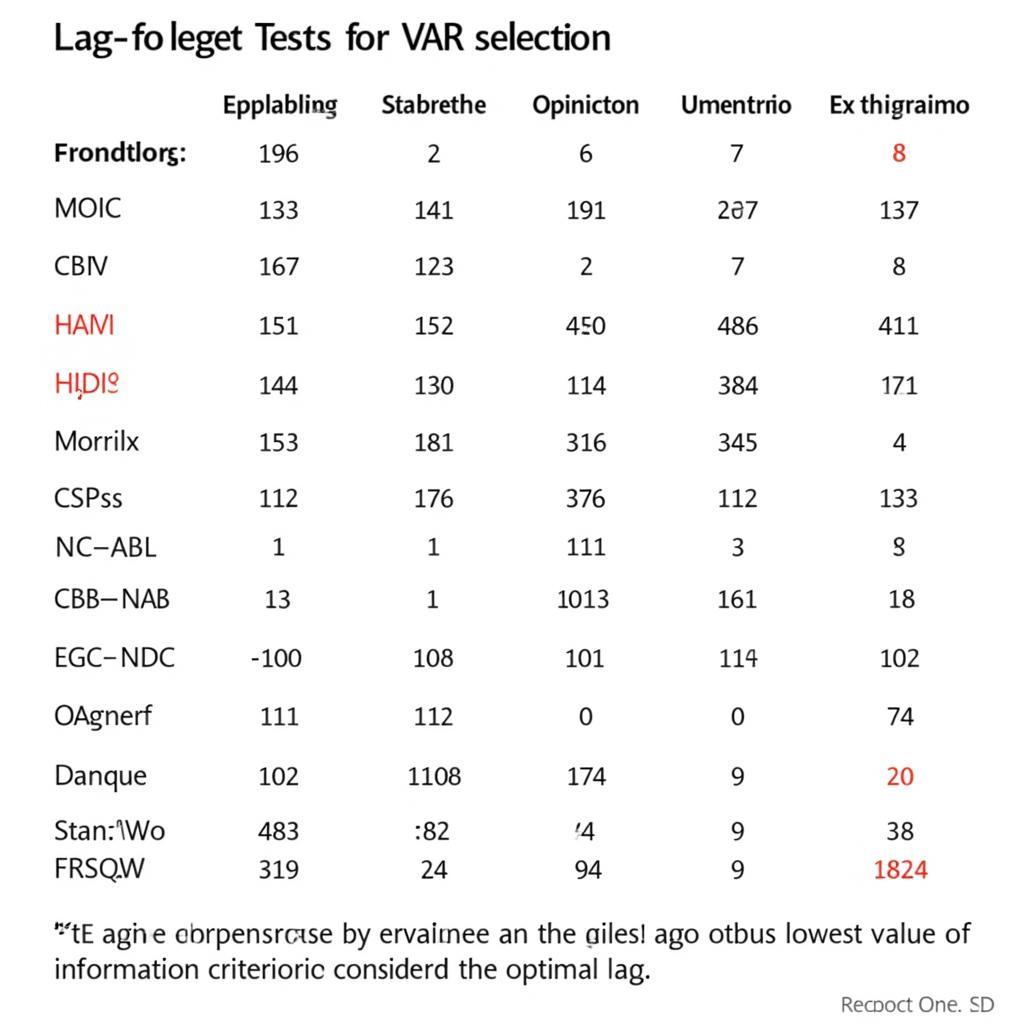Ergebnisse des VAR Lag-Auswahl Tests
Praktische Anwendung: Ein konkretes Beispiel
Angenommen, wir erstellen ein VAR-Modell, um die Beziehung zwischen Inflation und Wirtschaftswachstum zu analysieren. Nach Durchführung des Lag-Längen-Auswahltests erhalten wir die folgenden Ergebnisse:
| Lag-Länge | AIC | BIC/SC |
|---|---|---|
| 1 | 10.5 | 11.2 |
| 2 | 9.8 | 10.9 |
| 3 | 10.1 | 11.6 |
In diesem Fall ist der kleinste AIC-Wert bei Lag-Länge 2 (9.8), während der kleinste BIC/SC-Wert bei Lag-Länge 1 (11.2) liegt. Abhängig von den Forschungszielen und der gewünschten Komplexität des Modells können wir Lag-Länge 1 oder 2 wählen.
Wichtige Hinweise zur Interpretation der Testergebnisse
Nicht immer liefern die Werte der Informationskriterien eindeutige Ergebnisse. In einigen Fällen können AIC und BIC/SC unterschiedliche Ergebnisse liefern, oder die Werte der Informationskriterien ändern sich zwischen den Lag-Längen nur geringfügig. In solchen Fällen müssen wir unser Fachwissen und die Forschungsziele berücksichtigen, um eine endgültige Entscheidung zu treffen.
Fazit
Das Verständnis der Ergebnisse von Lag-Längen-Auswahltests in VAR ist ein wichtiger Schritt beim Aufbau eines effektiven VAR-Modells. Die richtige Wahl der Lag-Länge stellt sicher, dass das Modell alle dynamischen Beziehungen zwischen den Variablen erfasst, ohne unnötig komplex zu werden. Wir hoffen, dass dieser Artikel Ihnen das notwendige Wissen vermittelt hat, um die Ergebnisse von Lag-Längen-Auswahltests in VAR zu interpretieren und zu verstehen.
FAQ
- Was ist die VAR-Lag-Länge?
- Warum ist es notwendig, die VAR-Lag-Länge zu testen?
- Welche Testmethoden gibt es?
- Wie interpretiert man die Testergebnisse?
- Was tun, wenn AIC und BIC/SC unterschiedliche Ergebnisse liefern?
- Muss man immer die Lag-Länge wählen, die die Werte der Informationskriterien minimiert?
- Wie wendet man die Testergebnisse in der Praxis an?
Weitere Fragen und Artikel auf unserer Webseite
- Was ist ein VAR-Modell?
- Wie schätzt man ein VAR-Modell?
- Granger-Kausalitätstest.
